Wheatstone Bridge Method - Measurement of Medium Resistance

Wheatstone Bridge:

Wheatstone bridge is a very important device used in the measurement of medium resistances. A Wheatstone bridge has been in use longer than almost, any electrical measuring instrument. It is still an accurate and reliable instrument and is extensively used in the industry. Wheatstone bridge is an instrument for making comparison measurements and operates upon a null indication principle.

This means the indication is independent of the calibration of the null indicating instrument or any of its characteristics. For this reason, very high degrees of accuracy can be achieved using a Wheatstone bridge. The accuracy of 0.1% is quite common with a Wheatstone bridge as opposed to accuracies of 3% to 5% with the ordinary ohmmeter for measurement of medium resistances.

The figure below shows the basic circuit of a Wheatstone bridge. It has four resistive arms, consisting of resistances P, Q R and S together with a source of emf (a battery) and a null detector, usually a galvanometer G or other sensitive current meter. The current through the galvanometer depends on the potential difference between points c and d.

The bridge is said to be balanced when there is no current through the galvanometer or when the potential difference across galvanometer is zero. This occurs when the voltage from point b to point a equals the voltage from point d to point b or by referring to the other battery terminal when the voltage from point d to point c equals the voltage from point b to point c.

Must Read:

For a balanced condition, we can write,

I1 P = I2 R
The figure below shows the circuit for the Wheatstone bridge for the measurement of medium resistance.

measurement-of-medium-resistance-wheatstone-bridge , sensitivity-of-wheatstone-bridge

For the galvanometer current to be zero, the following conditions also exist:

where E = emf of the battery

Combining the above three equations we get,

from which
Q.R = P.S --->(4)

Equation-4 is the well-known expression for the balance of the Wheatstone bridge. If three of the resistances are known, the fourth may be determined from equation-4 and we obtain

R = S*(P/Q)

where R is the unknown resistance, S is called the 'standard arm' of the bridge and P and Q are called the 'ratio arms'.

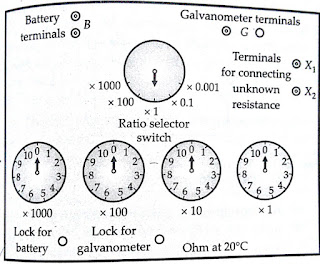
In the industrial and laboratory form of the bridge, the resistors which make up P, Q and S are mounted together in a box, the appropriate values being selected by dial switches. Battery and galvanometer switches are included together with a galvanometer and dry battery in the portable sets. P and Q normally consist of four resistors each, the values being 10,100,100 and 10,000Ω respectively S that decade arrangement of resistors. The below figure shows the commercial form of Wheatstone bridge for the measurement of medium resistance.

Sensitivity of Wheatstone Bridge:

It is frequently desirable to know the galvanometer response to be expected in a bridge which is slightly unbalanced so that a current flows in the galvanometer branch of the bridge network. This may be used for

(i) selecting a galvanometer with which a given unbalance may be observed in a specified bridge arrangement,

(ii) determining the minimum unbalance which can be observed with a given galvanometer in the specified bridge arrangement, and

(iii) determining the deflection to be expected for a given unbalance.

The sensitivity to unbalance can be computed by solving the bridge circuit for a small unbalance. The solution is approached by converting the Wheatstone bridge of the figure above to its "Thevenin Equivalent" circuit.

Assume that the bridge is balanced when the branch resistances are P, Q, R, S so that P / Q = R / S. Suppose the resistance R is changed to R+ΔR creating an unbalance. This will cause an emf 'e' to appear across the galvanometer branch. With the galvanometer branch open, the voltage drop between points a and b is :

The bridge sensitivity is defined as the deflection of the galvanometer per unit fractional change in unknown resistance.

Sensitivity of Wheatstone bridge,

From the above equation, it is clear that the sensitivity of the Wheatstone bridge is dependent upon bridge voltage, bridge parameters and the voltage sensitivity of the galvanometer. Rearranging the terms in the expression for sensitivity,

From the above equation, it is apparent that maximum sensitivity occurs where R / S = 1. As the ratio becomes either larger or smaller, the sensitivity decreases. Since the accuracy of measurement is dependent upon sensitivity a limit can be seen to the usefulness for a given bridge, battery and galvanometer combination.
For a bridge with equal arms, R=S=P=Q.

Bridge sensitivity , SB = (SV.E)/4

As explained above the sensitivity of Wheatstone bridge is maximum when the ratio is unity. The sensitivity with ratio P/Q = R/S = 1000 would be about 1/250 of that for unity ratio. The sensitivity with P/Q=R/S=1000 would similarly be about 1/250 of that for unity ratio.

Thus the sensitivity decreases considerably if the ratio P / Q = R / S is greater or smaller than unity. This reduction in sensitivity is accompanied by a reduction in accuracy with which a bridge can be balanced.

Galvanometer Current :

The current through the galvanometer can be found out by finding the Thevenin equivalent circuit. The Thevenin or open circuit voltage appearing between terminals b and d with galvanometer circuit open-circuited is,

The resistance of the Thevenin equivalent circuit is found by looking back into terminal c and d and replacing the battery by its internal resistance. In most cases, however, the extremely low resistance of the battery can be neglected and this simplifies the solution as we can assume that terminals a and b are shorted. The Thevenin equivalent resistance can be calculated by referring to the below figure.

Thevenin equivalent resistance of bridge ,

For a bridge with equal arms,

P = Q = S = R

R0 = R

The Thevenin equivalent of the bridge circuit, therefore, reduces to a Thevenin generator with an emf E0 and an internal resistance R0. Thevenin equivalent circuit of Wheatstone Bridge is shown below.

The current in the galvanometer circuit,

Ig = E0/(R0 + G)

Where G = resistance of the galvanometer circuit,